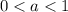Answer:
The required value of a is
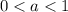
Explanation:
Given : Suppose the graph of the parent function
 is vertically compressed to produce the graph of the function
is vertically compressed to produce the graph of the function
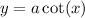 but there are no reflections.
but there are no reflections.
To find : Which describes the value of a?
Solution :
When the graph is vertically compressed by unit a
then the value of a lies between
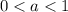
So, In the graph of parent function
 is vertically compressed to produce the graph of the function
is vertically compressed to produce the graph of the function
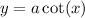 the value of a lies between
the value of a lies between
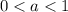 as there is no reflection so no changes.
as there is no reflection so no changes.
Therefore, The required value of a is