Given:
• Number of minutes they spent decorating together = 32 minutes.
,
• Baker A can decorate four times as fast as his new assistant.
Let's find the number of minutes it will take for each of them to decorate the cookies working individually.
Let x represent the number of minutes it will take the new assistant.
Let y represent the number of minutes it will take the baker.
Let the jobe be completed = 1
We have:
• y = 4x
,
• 32/x + 32/y = 1
Solve the system using substitution method.
Substitute 4x for y in equation 2.
We have the equation:
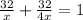
•
Let's solve the equation for x:
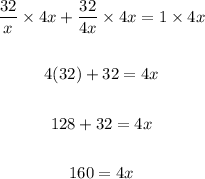
Solving further:
Divide both sides by 4
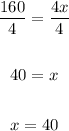
Substitute 40 for x in y = 4x
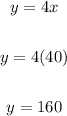
Therefore, we have the solution:
x = 40, y = 160
Therefore, it will take 40 minutes for the baker to decorate while it will take 160 minutes for his assistant.
ANSWER:
It will take 40 minutes for the baker to decorate while it will take 160 minutes for his assistant.