Question

Plutonium-240 decays according to the function where Q represents the quantity remaining after t years and k is the decay constant, 0.00011... How long will it take 24 grams of plutonium-240 to decay to 20 grams?

Answer 1

It will take 1,657.4 years.

Answer 2

1657.47 years

Explanation:

Let's find the answer by using the decay formula:

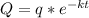`Q=q*e^(-kt)` where:

Q=quantity remaining after 't' years

q=initial amount

k=decay constant

t=time in years

Using the information provided by the problem we have:

`20=24*e^(-0.00011t)`

`ln(20/24)/(-0.00011)=t`

`1657.47=t`

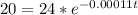
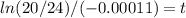
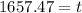
In conclusion, it will take 1657.47 years.