In the given figure above, we can use the formula for tangent-tangent angle. This is under the type of angle whose vertex is outside the circle and its sides intersects the circle.
Applying the tangent-tangent angle formula:
m∠APB =
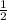
(ALB - AB)
m∠APB = angle of the vertex
ALB = measure of arc ALB
AB = measure of arc AB
we all know that the total measure of arc is equal to 360, hence, ALB + AB = 360
let: x = measure of arc AB
360 - x = measure of arc ALB
substitute:
78 =
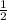
{(360 - x) - x}
78 =
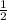
(360 - 2x)
78 = 180 - x ⇒ simplifying further by dividing both 360 and -2x by 2
x = 180 - 78 ⇒ combining like terms
x = 102
arc AB = 102 ⇒ Answer