Question

The slope of the line normal to the curve e^x-x^3+y^2 = 10 at the point (0, 3) is:

Answer 1

`\bf e^x-x^3+y^2=10\\\\ -----------------------------\\\\ e^x-3x^2++2y\cfrac{dy}{dx}=0\implies \cfrac{dy}{dx}=\cfrac{3x^2-e^x}{2y}`

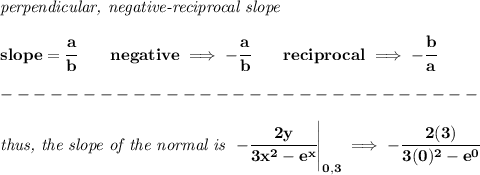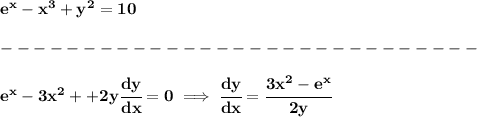
now, that's just the slope of that equation, now, what's the slope of a normal of it?

well, if you recall, a normal is just a perpendicular line to the tangent line at that same point, so the one above is the slope of a tangent line, the slope of a normal to a tangent, is the "negative reciprocal" of that

that is
`\bf \textit{perpendicular, negative-reciprocal slope} \\\\ slope=\cfrac{a}{{{ b}}}\qquad negative\implies -\cfrac{a}{{{ b}}}\qquad reciprocal\implies - \cfrac{{{ b}}}{a}\\\\ -----------------------------\\\\ \textit{thus, the slope of the normal is }\left. -\cfrac{2y}{3x^2-e^x} \right|_(0,3)\implies -\cfrac{2(3)}{3(0)^2-e^0}`