Question

The function f(t)= 7 cos((pi/4)t)+12 represents the tide in Light Sea. It has a maximum of 19 feet when time (t) is 0 and a minimum of 5 feet. The sea repeats this cycle every 8 hours. After 2 hours, how high is the tide?

Answer 1

The answer is 12 feet

Answer 2

The tide is 12 feet height at t=2.

Explanation:

Given:
`f(t)=7\cos((\pi)/(4)t)+12`

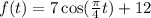
It is cosine function which represents the tide of light sea.

It has maximum of 19 feet at t=0

It has minimum of 5 feet at t=4

The sea repeats cycle every 8 hours. (Period = 8)

We need to find height of tide after 2 hours.

We will put t=2 into equation and solve for f(t)

`f(2)=7\cos((\pi)/(4)\cdot 2)+12`

`f(2)=7\cos((\pi)/(2))+12`

`f(2)=12`

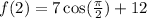
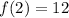
Please see the attachment for graphical result.

Hence, The tide is 12 feet height at t=2.