Question

Could someone please help me find the values for letters Z and Y for the first triangle? Thanks!

Answer 1

The right triangle is divided into two similar right triangles by the altitude, which is the side I named "h" in the sketch above. The hypotenuse of the triangle was divided into two segments "x" and "n". These segments have the following relationship with respect to the altitude:

`(x)/(h)=(h)/(n)`

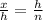
Given that we know the measures of "h" and "n" we can determine the measure of "x"

For h=12 and n=8:

`(x)/(12)=(12)/(8)`

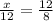
Multiply both sides by 12:

`\begin{gathered} 12\cdot(x)/(12)=12\cdot(12)/(8) \\ x=18 \end{gathered}`

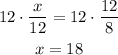
Now that we know the value of x, using the Pythagorean theorem we can determine the value of y. For the triangle on the left, the side "y" represents the hypothenuse:

This theorem states that the square of the hypothenuse of a right triangle is equal to the sum of the squares of the sides of the triangle, then:

`a^2+b^2=c^2`

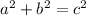
For our triangle:

`\begin{gathered} 18^2+12^2=y^2 \\ 324+144=y^2 \\ 468=y^2 \\ \sqrt[]{468}=\sqrt[]{y^2} \\ y=6\sqrt[]{13} \end{gathered}`

To determine the measure of side "z" you have to use the same method, considering the right triangle on the right, this side represents the hypothenuse. Use the Pythagorean theorem to calculate its length:

`a^2+b^2=c^2`

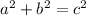
The sides of the triangle are h=12 and n=8

`\begin{gathered} 12^2+8^2=z^2 \\ 144+64=z^2 \\ 208=z^2 \\ \sqrt[]{208}=\sqrt[]{z^2} \\ z=4\sqrt[]{13} \end{gathered}`