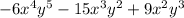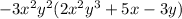Question

Factor the GCF: −6x4y5 − 15x3y2 + 9x2y3 (5 points)

Select one:
a. −3x2y2(2x2y3 − 5x + 3y)
b. −3x2y2(2x2y3 + 5x − 3y)
c. 3x2y2(2x2y3 + 5x − 3y)
d. −3(2x4y5 + 5x3y2 − 3x2y3)

Answer 1

-6x^4y^5-15x^3y^2+9x^2y^3

The GCF OF -6, -15, & 9, is -3
The GCF OF x's is x^2
The GCF OF y's is y^2
These are the number of x's and y's that each term has.
-3x^2y^2(2x^2y^3+5x-3y)
LETTER B

Answer 2

`-3x^2y^2(2x^2y^3+5x-3y)`

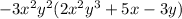
Explanation:

Factor the GCF:
`-6x^4y^5 - 15x^3y^2 + 9x^2y^3`

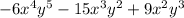
we find GCF for each term

GCF of -6, -15 and 9 is -3

For variables, the variable with lowest exponent is the GCF

GCF of x^4,x^3 and x^2 is x^2

GCF of y^5,y^2 and y^3 is y^2

So GCF is
`-3x^2y^2`

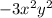
Now put GCF outside and divide each term by GCF

`-6x^4y^5 - 15x^3y^2 + 9x^2y^3`

`-3x^2y^2(2x^2y^3+5x-3y)`