Answer:
23rd term of A.P is 118.
Explanation:
Given that the first and ninth term of the arithmetic sequence which is 8 and 48 respectively.
we have to find 23rd term of A.P
The recursive formula for A.P is

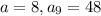
Put n=9, we get

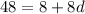
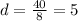
Now, twenty-third term is
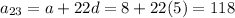
Hence, 23rd term of A.P is 118.
Option 2 is correct