Question

Find the area of the shaded sections. Click on the answer until the correct answer is showing.

it is a circle divided into 4 sections a radius of 4 and 2 arcs with 120 degree arcs i need to know what the smaller arcs are and the area

Answer 1

if it the circle with the x in it and the x is shaded i got 16/3pi

Answer 2

Hence, the area of shaded region is:

`(16\pi)/(3)`

Explanation:

We have to find the area of the smaller sectors that subtend an angle of 60° degree in the center.

Since the area of shaded portion is the area of circle excluding the area of smaller sectors.

We know that area of a sector is given as:

`Area=(1)/(2)r^2\phi`

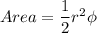
where φ is the angle in radians subtended to the center of the circle.

and r is the radius of the circle.

Now area of one sector with 60° angle is:

Firstly we will convert 60° to radians as:

`360\degree=2\pi\\\\60\degree=(2\pi)/(360)* 60\\\\60\degree=(\pi)/(3)`

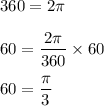
Hence, area of 1 sector is:

`Area=(1)/(2)* 4^2* (\pi)/(3)\\\\Area=(8\pi)/(3)`

Now, area of 2 sector is:

`Area=2* (8\pi)/(3)\\\\Area=(16\pi)/(3)`

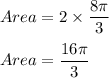
Hence, the area of shaded region is:

`(16\pi)/(3)`