Question

A dance instructor chose four of his 10 students to be on stage for a performance. If order does not matter, in how many different ways can the instructor choose the four students? 210 1,260 6,300 25,200

Answer 1

This is a combination in which you choose 4 from 10.
The formula is
combinations = 10! / 4! * (10-4)!
combinations = 10! / 4! * 6!
combinations = 10 * 9 * 8 * 7 * 6! / 4! * 6!
combinations = 10 * 9 * 8 * 7 / 4 * 3 * 2
combinations = 10 * 3 * 7
combinations = 210

Answer 2

Answer: First option is correct.

Step-by-step explanation:

Since we have given that

Number of students to be on stage for a performance = 10

Number of students to be choose by the instructor = 4

So, Number of ways to choose 4 students from 10 students is obtained by using " Combination " which says that

`^nC_r=(n!)/((n-r)!r!)\\\\where,\\\\n=\text{ number of students}\\\\and\\\\r=\text{ number of students chosen}`

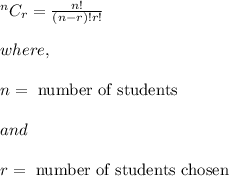
Now, according to our question, it becomes,

`^(10)C_4=(10!)/((10-4)!4!)\\\\^(10)C_4=(10!)/(6!* 4!)\\\\^(10)C_4=(10* 9* 8* 7)/(4* 3* 2)\\\\^(10)C_4=210`

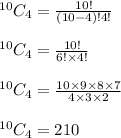
Hence, First option is correct.