Question

Which statement best explains whether the table represents a linear or nonlinear function? Input (x) Output (y) 2 5 4 10 6 15 8 20

Answer 1

The table represents a linear function because the rate of change is constant or all the points lie on a straight line.

Explanation:

Answer 2

The table represents a linear function because the rate of change is constant or all the points lie on a straight line.

Explanation:

From the given table it is noticed that the line passing through the points (2,5), (4,10), (6,15) and (8,20).

The slope of the line is

`m=(y_2-y_1)/(x_2-x_1)=(10-5)/(4-2)=(5)/(2)`

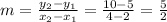
The slope of line is
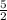`(5)/(2)`. It means the value of y increased by 5 if the value of x increased by 2.

From the given points we can noticed that the value of y increased by 5 if the value of x increased by 2. So, the function has same slope for any two points.

Since the rate of change (slope) is same for all points, therefore the table represents a linear function.

If we plot these points on a coordinate plane and connect then we get a straight line. I means it is a linear function.