Answer:
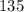
Step-by-step explanation:
Here, we want to know the number of seats that will be on the 6th row
The 6th row is simply 5 rows ahead of the first row
Since each row is 3 seats more than the last, we have the recursive formula as:

where:
an is the current row
an-1 is the row before the current
Finally, we have the number of seats as follows:
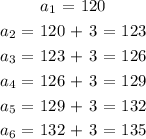
This means that, on the 6th row, we would have 135 seats