The given function is
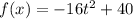
First, we find the vertex V(h,k), where
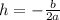
We know that a = -16 and b = 0, so
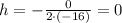
Then, we find k evaluating the function when x = 0.
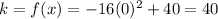
The vertex is V(0, 40).
Then, we find the intercepts of the function when y = 0.
![\begin{gathered} -16t^2+40=0 \\ -16t^2=-40 \\ t^2=-(40)/(-16) \\ t=\sqrt[]{2.5} \\ t\approx\pm1.58 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/fxfpns48ifcqg85kxics.png)
The intercepts are (-1.58, 0) and (1.58, 0).
Now, we use all three points to graph the function.
The image below shows the graph of the function:
In the image, we used t = x.