For investments compounded continuously, we have
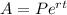
where P is the principal amount and A is the new amount after a period of time t.
Given the information that we have, we can solve for the time taken for the principal amount to reach $1000 as shown below.

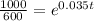
For powers of e, we can use the natural logarithmic function, ln(). Recall that
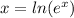
Using what we know, we can solve for t in our equation.
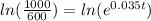
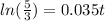
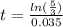
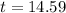
From this, we can see that it will take about 15 years for a principal amount of $600 to reach $1000 when compounded continuously at 3.5%.
Answer: 15 years