Question

A.If a new series is found by differentiating a known series with included endpoints, those endpoints might not be included in the new series. 

B.If a new series is found by differentiating a known series with included endpoints, those endpoints will never be included in the new series.
which statements are false?

Answer 1

Consider the power series


`\displaystyle\sum_(n\ge1)\frac{x^n}n`

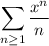
By the ratio test, this series converges for


`\displaystyle\lim_(n\to\infty)\left|(x^(n+1))/(n+1)\cdot\frac n{x^n}\right|=|x|\lim_(n\to\infty)\frac n{n+1}=|x|<1`

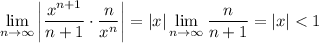
though we know by the alternating series test that the series converges for
`x=-1`.

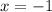
So this series converges for
`-1\le x<1`.

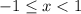
Differentiating the series yields


`\displaystyle(\mathrm d)/(\mathrm dx)\sum_(n\ge1)\frac{x^n}n=\sum_(n\ge1)x^(n-1)=\sum_(n\ge0)x^n`

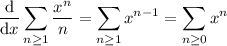
which is the geometric series. We know this series converges for
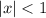
`|x|<1`, and this time the endpoints are not included.

This example shows that (A) is certainly possible; that is,
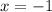
`x=-1` is valid in the first series, but not in the differentiated one.

- - -

Now consider the series


`\displaystyle\sum_(n\ge0)(x^n)/(n!)`

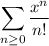
which we know to converge to
`e^x`.

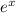
Differentiating, we get


`\displaystyle(\mathrm d)/(\mathrm dx)\sum_(n\ge1)(x^(n-1))/((n-1)!)=\sum_(n\ge0)(x^n)/(n!)=e^x`

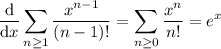
as expected. But both series converge everywhere, so this serves as a counter-example to the claim of B. So B is false.