Answer:
18569.234 years
Explanation:
Given : Carbon–14 is a radioactive isotope that decays exponentially at a rate of 0.0124 percent a year.
To Find: How many years will it take for carbon–14 to decay to 10 percent of its original amount?
Solution:
The equation for exponential decay is
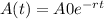
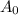 = initial amount
= initial amount
A(t) = Amount after t time
Now we are supposed to find after how many years will it take for carbon–14 to decay to 10 percent of its original amount.
So,
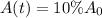
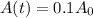
r = 0.0124 % = 0.000124
Substitute the values in the equation:
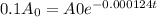
![- 0.000124t = ln [ (0.1 A_0)/( A_0)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/2d3hi284fppepp6zgw4sr129chmsqar9x8.png)
![t = ln [ (0.1 A_0)/( A_0)] * (1)/(- 0.000124)](https://img.qammunity.org/2018/formulas/mathematics/high-school/otaupzy5b5b84q6oher69ho525bl43cc7t.png)
![t = ln [0.1] * (1)/(-0.000124)](https://img.qammunity.org/2018/formulas/mathematics/high-school/kdml549xlj0yl5kqbxquk6arc5f2hrclaf.png)

Hence it will take 18569.234 years to decay to 10 percent of its original amount.