If the starting equation is
4²ˣ - 4 = 1
first move the 4 on the left to the right side:
4²ˣ = 5
Take the base-4 logarithm of both sides:
log₄(4²ˣ ) = log₄(5)
Drop the exponent on the left, using the property
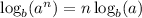 :
:
2x log₄(4) = log₄(5)
Now
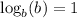 for any b, so
for any b, so
2x = log₄(5)
Solve for x by dividing both sides by 2:
x = 1/2 log₄(5)
You can also express this as
x = log₄(√5)
to make the solution slightly more compact.
You can also use the change-of-base identity to rewrite the solution as
x = log(5) / (2 log(4))
where the base of the logarithm is arbitrarily chosen. Then
x = log(5) / log(4²)
x = log(5) / log(16)
x = log₁₆(5)