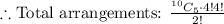Question

In how many ways can 10 people be seated across two tables, each seating five people?

Answer 1

To understand this problem, we need to first break it down. Assuming the tables are round, we can notice that this is a circular arrangement question.

We first need to assign five from a group of 10 people to a table. Since we don't care who appears on that table, we can use the notation:


`\text{Arrangements: } ^(10)C_5`

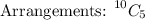
However, since they are not distinct tables, then we would have overcounted by a factor of 2!, since there are two tables. Thus, the total number of ways to assign the tables is:


`\text{Arrangements: } (^(10)C_5)/(2!)`

Now, we need to consider the total number of ways to arrange the people in each table. Since they are circular, then each table can be arranged in 4! ways.


`\therefore \text{Total arrangements: } (^(10)C_5 \cdot 4!4!)/(2!)`

`\therefore 72576 \text{ arrangements can be made.}`