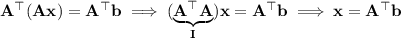Question

Find a formula for the least squares solution of ax=b when the columns of a are orthonormal1 .

Answer 1

Let
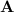
`\mathbf A` be a rectangular
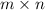
`m* n` matrix with column vectors
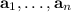
`\mathbf a_1,\ldots,\mathbf a_n`, i.e.


`\mathbf A=\begin{bmatrix}\mathbf a_1&\cdots&\mathbf a_n\end{bmatrix}`

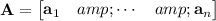
Then we have


`\mathbf A^\top=\begin{bmatrix}\mathbf a_1&\cdots&\mathbf a_n\end{bmatrix}^\top`

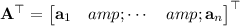
and the product of the two is


`\mathbf A^\top\mathbf A=\begin{bmatrix}\mathbf a_1\cdot\mathbf a_1&\mathbf a_1\cdot\mathbf a_2&\cdots&\mathbf a_1\cdot\mathbf a_n\\\mathbf a_2\cdot\mathbf a_1&\mathbf a_2\cdot\mathbf a_2&\cdots&\mathbf a_2\cdot\mathbf a_n\\\vdots&\vdots&\ddots&\vdots\\\mathbf a_n\cdot\mathbf a_1&\mathbf a_n\cdot\mathbf a_2&\cdots&\mathbf a_n\cdot\mathbf a_n\end{bmatrix}`

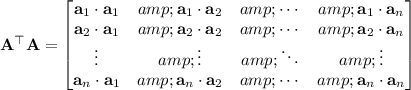
Because the columns of
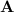
`\mathbf A` are orthonormal, we have


`\mathbf a_i\cdot\mathbf a_j=\begin{cases}1&\text{for }i=j\\0&\text{for }i\\eq j\end{cases}`

which means
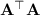
`\mathbf A^\top\mathbf A` reduces to an
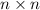
`n* n` matrix with ones along the diagonal and zero everywhere else, i.e.


`\mathbf A^\top\mathbf A=\begin{bmatrix}1&0&\cdots&0\\0&1&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&1\end{bmatrix}=\mathbf I_n`

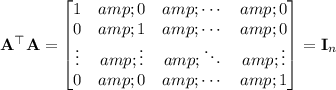
where
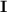
`\mathbf I` denotes the identity matrix. This means the solution to
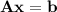
`\mathbf{Ax}=\mathbf b` is given by


`\mathbf A^\top(\mathbf{Ax})=\mathbf A^\top\mathbf b\implies(\underbrace{\mathbf A^\top\mathbf A}_(\mathbf I))\mathbf x=\mathbf A^\top\mathbf b\implies\mathbf x=\mathbf A^\top\mathbf b`