Answer: 98.33 - 101.67
Explanation:
The given Sample mean n= 100
Standard deviation

Mean IQ in the sample
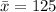
Standard error of mean =
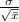
Standard error of mean =
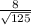
Thus, standard error =
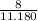
Standard error of mean (SE)= 0.7155
We know that z - score for 98% confidence interval is 2.33 .
Now, 98% confidence interval will be
n-z(SE) and n+z(SE)
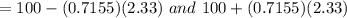


Hence, the 98% confidence interval for the students' mean IQ score will be 98.33 - 101.67