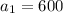Question

Paige borrows $700 from her parents for a new computer. She repays $100 the first month, then begins to repay her parents $75 per month. Which recursive formula models the total amount of money still owed, mc022-1.jpg?

Answer 1

The recursive formula that models the amount owed is
an = a(n-1) -75; a1 = 600.
This formula is for AFTER the first month of payment, this is why the first term is 700-100 = 600. This also means that n > 1.

Answer 2

Option B is correct

`a_n = a_(n-1)-75` ;
`a_1 = 600`

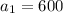
Explanation:

The recursive formula for the arithmetic sequence is given by:

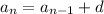`a_n = a_(n-1)+d` .....[1]

where,

d is the common difference.

n is the number of terms.

As per the statement:

Paige borrows $700 from her parents for a new computer.

She repays $100 the first month, then begins to repay her parents $75 per month.

Now, she only has to pay back after then, $700 - $100 = $600

then, begins to repay her parents $75 per month.

The sequence we get;

600, 525, 450, ....

This is the arithmetic sequence.

here,
`a_1 = 600`

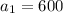
and d = -75

Since,

525-600 = -75

450-525 = -75 and so on...

Substitute the given values in [1] we have;

`a_n = a_(n-1)-75`

Therefore, the recursive formula models the total amount of money still owed is:

`a_n = a_(n-1)-75` ;
`a_1 = 600`