Answer:
One point could be (1,1)
Explanation:
1. The equation of the circle is
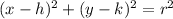
h and k are the (x,y) coordinates of the center of the circle respectively. In this sense, h=6 and k=1, and r is the radius of the circle which is 5. Replacing we get

2. The x-coordiante of the center of the circle is at x=6. The radius is 5, therefore, the left end of the circle is at x=1 and the right end is at x=11. This means that the circle can take x-coordiantes from 1 to 11, and for each we will have a Y-coordinate.
3. To get the Y-coordinate we isolate Y from the circle equation.
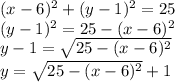
4. From the last equation, we can repalce x by any number between 1 and 11, and we will get the respective Y-coordinate, for example:
If we take x=1, replacing we get:
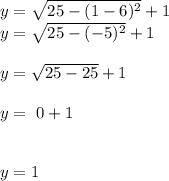
So, one point could be (1,1)
5. If you want to get another point, you could replace X by 2,3,4,5,6,7,8,9,10 and 11 in the previous equation, and for each one you will get a new Y-coordinate.