Question

Use the first derivative test to classify the relative extrema

Answer 1

Local maximum: (-1/5, -10)

Local minimum: (1/5, 10)

Step-by-step explanation:

Given the below function;

`f(x)=(25x^2+1)/(2)`

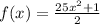
To determine the relative maxima of the above function using the First Derivative Test, we'll follow the below steps;

Step 1: Determine the derivative of f(x) using the Quotient rule;

Let u = 25x^2 + 1

u' = 50x

Let v = x

v' = 1

`\begin{gathered} f^(\prime)(x)=(v\cdot u^(\prime)-u\cdot v^(\prime))/(v^2)_{} \\ f^(\prime)(x)=(x(50x)-(25x^2+1)(1))/(x^2) \\ f^(\prime)(x)=(25x^2-1)/(x^2) \end{gathered}`

Step 2: Determine the critical points by equating f(x) to zero and solving for x;

`\begin{gathered} (25x^2-1)/(x^2)=0 \\ 25x^2-1=0 \\ 25x^2=1 \\ x^2=(1)/(25) \\ x=\pm\sqrt[]{(1)/(25)} \\ x=\pm(1)/(5) \end{gathered}`

Step 3: Since the critical points are at -1/5 and 1/5, we'll check if the first derivative changes signs around these points by picking numbers from different intervals as seen below;

From negative infinity to -1/5, let's pick -1;

`f^(\prime)(-1)=(25(-1)^2-1)/((-1)^2)=(25-1)/(1)=24`

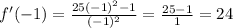
From -1/5 to 1/5, let's pick 0.1;

`f^(\prime)(0.1)=(25(0.1)^2-1)/((0.1)^2)=-75`

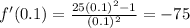
From 1/5 to infinity; let's pick 1;

`f^(\prime)(1)=(25(1)^2-1)/((1)^2)=24`

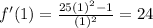
We can see from the above that the first derivative changes from positive to negative around x = -1/5, it signifies that this critical point is a local maximum.

It also changes from negative to positive around x = 1/5, it signifies that this critical point is a local minimum.

Let's go ahead and determine the actual points at which the function has the local minimum and maximum by evaluating f(x) at the critical points;

`\begin{gathered} f(-(1)/(5))=(25(-(1)/(5))^2+1)/((-(1)/(5)))=-10 \\ f((1)/(5))=(25((1)/(5))^2+1)/(((1)/(5)))=10 \end{gathered}`

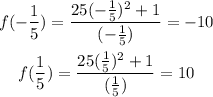
Therefore, the function f(x) has a local maximum at (-1/5, -10) and a local minimum at (1/5, 10)