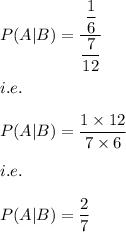Question

according to the general equation for conditioning probability if P(A^B)=1/6 and P(B)=7/12 what is P(A / B)

Answer 1

Assuming P(A^B) is the same as
`\mathbb P(A\cap B)` and P(A/B) means
`\mathbb P(A|B)`, by the definition of conditional probability we have


`\mathbb P(A|B)=(\mathbb P(A\cap B))/(\mathbb P(B))\iff\mathbb P(A|B)=\frac{\frac16}{\frac7{12}}=\frac27`

Answer 2

Hence,

`P(A|B)=(2)/(7)`

Explanation:

Two events are given by A and B.

Conditional probability--

It is the probability of an event given that the other event has already occurred.

We know that the conditional probability that is P(A|B) is calculated by using the formula:

`P(A|B)=(P(A\bigcap B))/(P(B))`

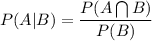
Also,

Conditional probability that is P(B|A) is calculated by using the formula:

`P(B|A)=(P(A\bigcap B))/(P(A))`

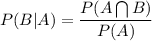
Here we are asked to find:

P(A|B)

Given that:

`P(B)=(7)/(12)\ and\ P(A\bigcap B)=(1)/(6)`

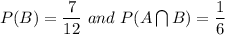
Hence,

`P(A|B)=((1)/(6))/((7)/(12))\\\\i.e.\\\\P(A|B)=(1* 12)/(7* 6)\\\\i.e.\\\\P(A|B)=(2)/(7)`