Question

Compute the sums below. (Assume that the terms in the first sum are consecutive terms of an arithmetic sequence.)

Answer 1

The given sequence is

From the sequence it follows

`a=8,d=-3`

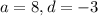
The formula for sum of an arithmetic sequence

`S=(n)/(2)(a+l)`

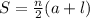
Since the number of terms is not given then

Using the nth term formula

`a_n=a+(n-1)d`

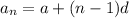
Substitute

`a_n=-403,a=8,d=-3`

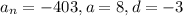
Into the nth term formula

`\begin{gathered} -403=8+(n-1)-3 \\ -403=8-3n+3 \\ -403-11=-3n \\ -3n=-414 \\ n=138 \end{gathered}`

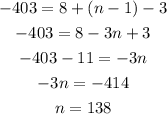
Therefore the sum is

`\begin{gathered} S=(138)/(2)(8+(-403)) \\ S=69(-395) \\ S=-27255 \end{gathered}`

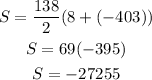
Therefore the solution is:

`S=-27255`