We are asked to determine the surface area of two cylinders. To do that we will determine the area of the sides of the cylinders and the area of the top and bottom parts.
The are of the side of the cylinder is given by the following formula:
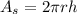
Where:

For the first cylinder, we have a diameter of 7cm. Since the radius is half the diameter we have:
![r_1=\frac{7\operatorname{cm}}{2}=3.5\operatorname{cm}]()
Substituting we get:
![A_s=2\pi(3.5\operatorname{cm})(122\operatorname{cm})]()
Solving the operations:
![A_s=2682.92\operatorname{cm}^2]()
The are of the top and bottom parts is the area of a circle and is given by:
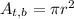
Since the two parts are equal we will multiply the formula by 2:
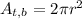
Substituting the values we get:
![A_(t,b)=77\operatorname{cm}^2]()
Now, we add both areas to get the total surface area of the cylinder:
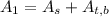
Substituting we get:
![A_1=2682.92\operatorname{cm}^2+77cm^2]()
Solving the operations:
![A_1=2759.89\operatorname{cm}^2]()
Therefore, the first tube requires 2759.89 cm^2 of plastic.
Now, we use the same procedure to determine the surface area of the second tube. First, we determine the area of the second tube:
![r_2=\frac{11\operatorname{cm}}{2}=5.5\operatorname{cm}]()
Now, we use the formula for the area of the side:
![A_s=2\pi(5.5\operatorname{cm})(85\operatorname{cm})]()
Solving the operations:
![A_s=2937.39\operatorname{cm}^2]()
Now we determine the areas of the top and the bottom:
![A_(t,b)=\pi(5.5\operatorname{cm})^2]()
Solving the operations:
![A_(t,b)=95\operatorname{cm}^2]()
Now, we determine the total surface area:
![A_2=2937.39cm^2+95\operatorname{cm}^2]()
Solving the operations:
![A_2=3032.42\operatorname{cm}^2]()
Therefore, since:
![\begin{gathered} 3032.42\operatorname{cm}>2937.39\operatorname{cm}^2 \\ A_2>A_1 \end{gathered}]()
This means that the second tube requires more plastic.