Question

A farmer has 25 yards of fencing to make a pig pen. He is going to use the side of the barn as one of the sides of the fence, so he only needs to fence 3 sides. What should be the dimensions of the fence in order to maximize the area?

4 yards by 17 yards
B) 5 yards by 15 yards
C) 6.25 yards by 12.5 yards
D) 13.25 yards by 13.5 yards

Answer 1

which ever one adds up to 25 yds :)

Answer 2

By simply calculating the areas you can easily find that C is the largest (78.125). But let's approach this one mathematically:

If the side of the fence opposite of the barn has length a, and the sides perpendicular to the barn has length b, we know that:


`a + 2b = 25 \implies a = 25-2b`

And we want to maximize a x b.

Filling in the expression for a in the area, we actually want to maximize:


`(25 - 2b) \cdot b = -2 b^(2) + 25b`

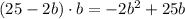
This is a mountain parabola. To find its maximum, we equal the derivative to 0:


`25 - 4b = 0 \implies b=6.25`

From this follows a = 12.5, but now we have proven that C is really the optimum!