Question

No matter the diameter most pizzas have a 1 inch thick crust. For each size determine how much is the cheesy inside part and how much is the crust. Q: As the pizza gets smaller, what happens to the fraction

Ali Abu Harb asked Oct 24, 2023

438,002 views

1 Answer

Ask a Question

Sdffadsf · Answer 1 · 2023-10-29T18:52:51+0000

For each diameter size, we need to find the inside area and the crust area. Also, we need to consider that the crust is always 1 inch on either side of the pizza.

For the 14-inch diameter pizza:

The following diagram represents what we know about the pizza:

We can see that the diameter of the pizza is 14 inches, and the crust is 1 inch.

Thus, to find the inside area, we need the diameter of the inside part of the pizza. So we subtract 1 to the diameter on each side, and as we can see in the following image, the diameter of the inside part (represented in blue) is 12 inches:

With this diameter, we can calculate the area with the following formula:

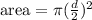
$\text{area}=\pi((d)/(2))^2$

Thus, to find the inside area, we substitute the diameter of the inside area which is d=12in

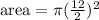
$\text{area}=\pi((12)/(2))^2$

Solving the operations, and substituting pi=3.1416:

$\begin{gathered} \text{Inside area }=3.1416(6)^2 \\ \text{Inside area =3.1416(36)} \\ \text{Inside area =113.0976in}^2 \end{gathered}$

Now that we have the inside area, we can calculate the crust Area.

The crust area can be found by subtracting the inside area from the total area:

The blue part in the last image is the inside area, and as you can see, when we subtract that blue area from the total area of the pizza, we get only the crust part of the area.

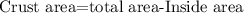
$\text{Crust area=total area-Inside area}$

We know the inside area, but we need to find the total area before calculating the crust are.

So we use d=14in in the formula for the area:

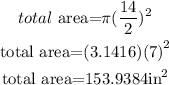
$\begin{gathered} total\text{ area=}\pi((14)/(2))^2 \\ \text{total area=(3.1416)(7)}^2 \\ \text{total area=153.9384in}^2 \end{gathered}$

Finally, we subtract the inside area from the total area and we find the crust area:

$\begin{gathered} \text{crust area=total area - Inside area} \\ crustarea=153.9384in^2\text{-113.0976in}^2 \\ \text{crust area=40.841in}^2 \end{gathered}$

In summary, for the first pizza:

Inside area (in^2): 113.0976

Crust area (in^2): 40.841

For the 12-inch diameter pizza:

We follow the same procedure that we did for the first pizza.

Subtract 1inch to each side of the pizza to find the inside diameter:

The diameter of the inside area in this case is 12inches, now we use this diameter in the area formula:

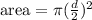
$\text{area}=\pi((d)/(2))^2$
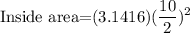
$\begin{gathered} \text{Inside area=(3.1416)(}(10)/(2))^2 \\ \end{gathered}$

Solving the operations:

$\begin{gathered} \text{Inside area=(3.1416)(5})^2 \\ \text{Inside area=(3.1416)(25)} \\ \text{Inside area=}78.54in^2 \end{gathered}$

Now, we find the total area to subtract from it the inside area and find the crust area. For the total area we use the diameter of 12 inches:

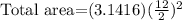
$\text{Total area=(}3.1416)((12)/(2))^2$

Solving the operations:

$\begin{gathered} \text{Total area=(3.1416)(6)}^2 \\ \text{Total area=(3.1416)}(36) \\ \text{Total area=}113.0976in^2 \end{gathered}$

And the crust area:

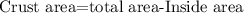
$\text{Crust area=total area-Inside area}$
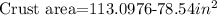
$\text{Crust area=113.0976-}78.54in^2$
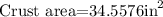
$\text{Crust area=34.5576in}^2$

In summary for the second pizza:

Inside area(in^2): 78.54

Crust area(in^2): 34.5576

For the 6-inch diameter pizza

The total diameter is 6 inch, so the total area is:

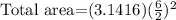
$\text{Total area=(3.1416)(}(6)/(2))^2$

Solving the operations:

$\begin{gathered} \text{Total area=(3.1416)(3})^2 \\ \text{Total area=(3.1416)}(9) \\ \text{Total area=}28.2744in^2 \end{gathered}$

For the inside area, we do the same thing that we did in the last two pizzas, we subtract 1 inch to each side, so if this pizza has 6 inches of diameter, the inside part has a diameter of 6-2=4inches.

So we calculate the area for the inside part with the diameter of 4 inches:

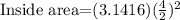
$\text{Inside area=(3.1416)(}(4)/(2))^2$

Solving the operations:

$\begin{gathered} \text{Inside area=(3.1416)}(2)^2 \\ \text{Inside area=(3.1416)(4)} \\ \text{Inside area=}12.5664in^2 \end{gathered}$

We have the inside area, now we subtract it from the total area to find the crust area:

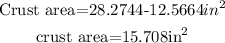
$\begin{gathered} \text{Crust area=28.2744-12.5664}in^2 \\ \text{crust area=15.708in}^2 \end{gathered}$

In summary for the third pizza:

Inside area (in^2): 12.5664

Crust area (in^2): 15.708