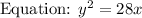Question

Write an equation of a parabola that opens to the right, has a vertex at the origin, and a focus at (7, 0.

Answer 1

If a parabola opens to the right, then we know it is with respect to y and it's positive.

With vertex (h, k), we can write the equation as:

`(y - k)^(2) = 4a(x - h)`

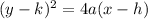
Replacing (h, k) with (0, 0), we get:

`y^(2) = 4ax`

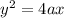
Now, the focus is a point (a, 0) on the parabola, such that its length from any point on the parabola is equidistant to the moving point on the parabola and the directrix, often noted as: x or y = -a

We're given the focus is: (7, 0)
The focus in its most general term is (a, 0), for when the vertex is at the origin.
Thus a = 7.


`\text{Equation: } y^(2) = 28x`