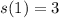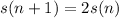Question

Find and solve a recurrence relation for the number of n-digit ternary sequences with no con-secutive digits being equal.

Answer 1

It sounds very difficult but I think it actually is quite simple.

For a sequence of ternary digits (ie., use symbols 0, 1 and 2), you have the freedom to choose the first digit as you like, but for all the other digits, you can only choose the 2 alternatives you have.

So for n digits the number of sequences is:


`s(n) = 3 \cdot 2^(n-1) , n \in \mathbb{N} _(1)`

Rewriting this as a recurrence relation:


`s(1)=3`

`s(n+1) = 2s(n)`