Question

What is the sum of the first 6 terms of this geometric sequence?–4, –16, –64, –256, …a.–1024b.–4096c.–5460d.–5476?

Answer 1

`\text{Sum to n terms of geometric series: } S_n = (a(r^(n) - 1))/(r - 1)}, r \\eq 1`

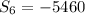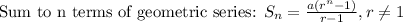
We know that a is equal to the first term, r represents the common ratio, and n represents the number of terms.

a = -4
n = 6

To find r:

`(-16)/(-4) = (-64)/(-16)`

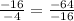
Since we do have a common ratio of 4, then we know it is a geometric sequence. Substituting everything in, we get:


`S_6 = (-4(4^(6) - 1))/(4 - 1)`

`S_6 = (-4(4096 - 1))/(3)`

`S_6 = (-4(4095))/(3)`

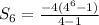
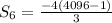
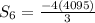
By calculator, we get:

`S_6 = -5460`