Question

How will the area of the circle change if it is dilated by a scale factor of 1/2

Answer 1

The circle would get smaller.

Answer 2

Answer: The area of the dilated circle will be one-forth of the area of the original circle.

Step-by-step explanation: We are given to find the change in area of a circle if it is dilated by a scale factor of half.

Let r represents the RADIUS and A represents the AREA of the circle before dilation.

And, r' represents the radius and A' represents the AREA of the circle after dilation.

So, we get

`A=\pi r^2~~~~~~\textup{and}~~~~~~A'=\pi r'^2.`

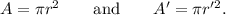
In case of a circle, scale factor is the ratio of the radius of the dilated circle to the radius of the original circle.

That is,

`(1)/(2)=(r')/(r)\\\\\\\Rightarrow r'=(r)/(2).`

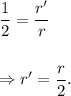
Therefore, the area of the dilated circle will be

`A'=\pi r'^2=\pi *\left((r)/(2)\right)^2=(\pi r^2)/(4)=(1)/(4)* A.`

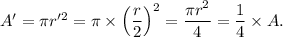
Thus, the area of the dilated circle will be one-forth of the area of the original circle.