Question

Let R be the region in the plane bounded by y=x^2, y=0, and x=1. Set

up an iterated double integral to evaluate double integral of e^(y/x)

Answer 1

One way to set up the integral is to write it as


`\displaystyle\iint_Re^(y/x)\,\mathrm dA=\int_(x=0)^(x=1)\int_(y=0)^(y=x^2)e^(y/x)\,\mathrm dy\,\mathrm dx`

In the opposite order, you could use the equivalent


`\displaystyle\iint_Re^(y/x)\,\mathrm dA=\int_(y=0)^(y=1)\int_(x=\sqrt y)^(x=1)e^(y/x)\,\mathrm dx\,\mathrm dy`

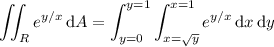
It's not clear whether you actually have to evaluate the integral or not; I suspect no, since either integrand taken with respect to
`x` does not have an elementary antiderivative.