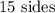Answer:
The number of sides the garden has is:
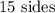
Step-by-step explanation:
Given that each exterior angle of a regular polygon of sides n is equal to
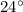
Recall that the sum of exterior angles of a polygon is equal to 360 degrees.
For a n sided regular polygon with each exterior angle equal to 24 degrees, we have;
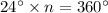
let us solve for n by dividing both sides by 24 degrees;
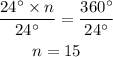
Therefore, the number of sides the garden has is: