Answer:
The z-score value of the data is -0.838.
Explanation:
Given : A mean of 7.6 and a standard deviation of 3.1.
To find : How many standard deviations of the mean do the values 10, 9, 11, 5, and 3 fall?
Solution :
Mean
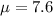
Standard deviation
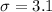
Values 10, 9, 11, 5, and 3 i.e. x=5
The z-score value for x=5 is given by
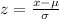
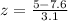
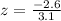
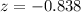
The z-score value of the data is -0.838.