Question

What system of equation is this x+y-4=0 x-y=0 the solution is in the quadrant.?

Answer 1

• (x,y)=(2,2)

,

• Quadrant I

Step-by-step explanation:

Given the system of equations:

`\begin{gathered} x+y-4=0 \\ x-y=0 \end{gathered}`

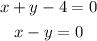
We are required to solve the system graphically.

To do this, find two points on each of the lines.

(a)x+y-4=0

When x=0

`\begin{gathered} x+y-4=0 \\ 0+y-4=0 \\ y=4 \\ \implies(0,4) \end{gathered}`

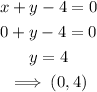
When x=1

`\begin{gathered} x+y-4=0 \\ 1+y-4=0 \\ y-3=0\implies y=3 \\ \implies(1,3) \end{gathered}`

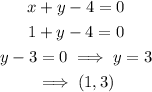
Join the points (0,4) and (1,3) to plot the first equation.

(b)x-y=0

When x=0, y=0 ==>(0,0)

When x=2, y=2 ==>(2,2)

Join the points (0,0) and (2,2) to plot the second equation.

The graph is shown below:

The two lines intersect at (2,2).

Therefore, the solution to the system of equations is:

`(x,y)=(2,2)`

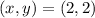
The solution (2,2) is in Quadrant I.