Question

How many complex roots does the equation below have? X^6+x^3+1=0

Answer 1

If you find the discriminant it will tell you the number and types of roots. The discriminant is the value b^2 -4ac.
a = 1
b = 1
c = 1
1^2 - 4*1*1
1-4 = -3
Since this is a negative number there will be 2 complex roots.

Answer 2

The number of complex roots is 6.

Explanation:

The given equation is

`x^6+x^3+1=0`

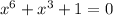
it can be written as

`(x^3)^2+x^3+1=0`

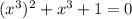
Substitute
`t=x^3`,

`(t)^2+t+1=0`

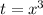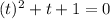
Using quadratic formula.

`t=(-1\pm √(1^2-4(1)(1)))/(2)=(-1\pm 3i)/(2)`
`t=(-b\pm √(b^2-4ac))/(2)`

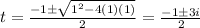
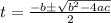
We know that

`\omega =(-1\pm 3i)/(2)`

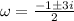
It is a complex number.

`x^3=\omega`

`x=(\omega)^{(1)/(3)}`

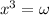
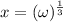
Cube root of a complex number is complex.

Therefore the number of complex roots is 6.