Given n = 4, p = 25 % , q= 1- p
since 25% of all prison parolees become repeat offenders
![\begin{gathered} \text{success = does not become repeat offender} \\ p\text{= 1-25\%} \\ q=1-(25)/(100)=(75)/(100) \end{gathered}]()
(a) Consider that the random variable X follows a binomial distribution with parameters n and p. So, the binomial probability is,
The probability of x successes in n trials is:
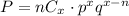
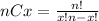
Here, r is the number of successes that results from the binomial experiment, n is the number of trials in the binomial experiment, and p is the probability of success on an individual trial. Thus, the probability of exactly 3 successes in 4 trials can be computed as:
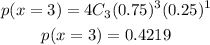
The probability of exactly 3 successes = 0.4219
(b) The expected number of parolees in Alice group will not be repeat offenders = 3
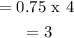
(c) Standard deviation = 0.8660
![\begin{gathered} \sigma=\sqrt[]{npq} \\ \sigma=\sqrt[]{4*0.75*0.25} \\ \sigma=0.8660 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/vfly5g4hdhjayb8na1hm.png)