Question

Parole USA Today reports that about 25% of all prison parolees become repeat offenders. Alice is a social worker whose job is to counsel people on parole. Let us say success means a person does not become a repeat offender. Alice has been given a group of four parolees.a) find the probability of exactly 3 successes.b) What is the expected number of parolees in Alice's group who will not be repeat offenders? What is the standard deviation?

Answer 1

Given n = 4, p = 25 % , q= 1- p

since 25% of all prison parolees become repeat offenders

(a) Consider that the random variable X follows a binomial distribution with parameters n and p. So, the binomial probability is,

The probability of x successes in n trials is:

`P=nC_x_{}\cdot p^xq^(x-n)`
`nCx=(n!)/(x!n-x!)`

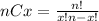
Here, r is the number of successes that results from the binomial experiment, n is the number of trials in the binomial experiment, and p is the probability of success on an individual trial. Thus, the probability of exactly 3 successes in 4 trials can be computed as:

`\begin{gathered} p(x=3)=4C_3(0.75)^3(0.25)^1 \\ p(x=3)=0.4219 \end{gathered}`

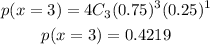
The probability of exactly 3 successes = 0.4219

(b) The expected number of parolees in Alice group will not be repeat offenders = 3

`\begin{gathered} =0.75\text{ x 4 } \\ =3 \end{gathered}`

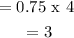
(c) Standard deviation = 0.8660

`\begin{gathered} \sigma=\sqrt[]{npq} \\ \sigma=\sqrt[]{4*0.75*0.25} \\ \sigma=0.8660 \end{gathered}`