Question

The doubling period of a bacterial population is 15 minutes. At time t=120 minutes, the bacterial population was 60000.A) What was the initial population at time t=0?B) Find the size of the bacterial population after 3 hours

Answer 1

If you follow the formula

`y=ab^t`

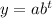
Where y is the total amount of bacteria, a is the initial bacterial at time 0, and b is the growth factor.

A) At t=120 minutes. This would be 15 minutes 8 times. So the time for t=8:

`\begin{gathered} 60000=a(2)^8 \\ 60000=a(256) \\ (60000)/(256)=(a(256))/(256) \\ a=234.375 \end{gathered}`

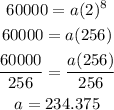
Answer a: the initial population = 234.375

B) The equation is given by:

`y=234.375(2)^t`

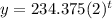
After 3 hours (15 minutes, 12 times), or at t = 12 you would get:

`y=234.375(2)^(12)=960000`

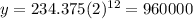
Answer b: the bacterial population = 960000