Answer:
The value of P(7, 1) is 7.
Explanation:
Given : P( 7, 1)
We have to evaluate the value of P(7, 1)
Consider the given P(7, 1)
 is defined as the number of the possibility of choosing an ordered set of r objects from a total of n objects.
is defined as the number of the possibility of choosing an ordered set of r objects from a total of n objects.
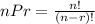
Put n = 7 and r = 1 , we have,
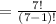
Simplify, we have,

Thus, The value of P(7, 1) is 7.