Question

Multiply or divide as indicated b^7/b^6

Answer 1

b^7/b^6 is dividing b^7 by b^6. When dividing exponents, you are subtracting them. Basically, you are subtracting 6 from 7.
Your answer is to divide, and the quotient is b^1 or just b.
I hope this helps!

Answer 2

`(b^(7))/(b^(6))=b`

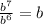
Explanation:

Hello, I think I can help you with this.

Let's remember some properties of potentiation

`a^(0)=1\\a^(1)=a\\( (a)/(b))^(2)=(a^(2))/(b^(2)) \\\\( (a)/(b))^(-1)=(b)/(a)\\\\(a^(n))/(a^(m)) =a^(n-m)\\`

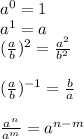
Step 1

define

in this case we have a division of two potents with the same base.

according to the last equation

let

`(a^(n))/(a^(m)) =a^(n-m) \\a=b\\n=7\\m=6\\`

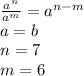
Step 2

replace

`(b^(7))/(b^(6)) =b^(7-6)\\=b^(1)=b\\ hence\\}\\(b^(7))/(b^(6))=b`

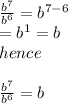
Have a good day