Question

The area of a rectangle is 5x^3+19x^2+6x-18 with length x + 3. Using synthetic division, what is the width of the rectangle?

Answer 1

A

Explanation:

For edge

Answer 2

To compute for the area of the rectangle, we multiply the dimensions so if we need to find the width of the rectangle, we have


`width = (Area)/(length)`

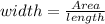
Thus, given an area of (5x³ + 19x² + 6x - 18) and a length of (x + 3), to find the width, we have

width = (5x³ + 19x² + 6x - 18) / (x + 3)

Through the coefficients of the polynomial, we can apply synthetic division to find the quotient as shown below.

5 19 6 -18 | -3
-15 -12 18
_____________
5 4 -6 0

Thus, the given values below the line are the coefficients of the width. So, we have the rectangle's width as (5x² + 4x - 6) units.

Answer: (5x² + 4x - 6) units