Answer:
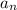 = 6 − 4(n − 1); all integers where n ≥ 1
= 6 − 4(n − 1); all integers where n ≥ 1
Explanation:
An arithmetic sequence is a sequence in which the difference between each consecutive term is same and this difference is called common difference.
Also, it can be defined by explicit formula,
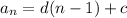 ,
,
where d is the common difference and c is the first term of the A.P.
Here, first term, c = 6,
And, second term = 2,
So, the common difference, d = Second term - First term = 2 - 6 = -4,
Thus, the explicit formula for the given A.P. is,
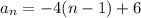
Or
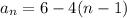
Since, the domain of an A.P. is always the set of all natural numbers,
So, Domain of the given A.P. is 1 ≤ n,
Hence, the LAST OPTION is correct.