Question

The function below represents the number of zombies, N, where t is the number of years since the zombies gained control of Earth: N(t) = 300 · 2-t/8 Is this exponential growth or decay? Explain using your understanding of the properties of exponents. (To type exponents, use the ^ key.)

Answer 1

This is decay. The exponent has a negative sign. The reciprocal of 2 is 0.5. So N(t) can be rewritten as 0.5^(t/8). The base is fraction less than 1, which is decay.

Answer 2

The given function is exponential decay.

Explanation:

Given : The function below represents the number of zombies, N, where t is the number of years since the zombies gained control of Earth :
`N(t)=300\cdot 2^{-(t)/(8)}`

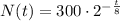
To find : Is this exponential growth or decay?

Solution :

Exponential function is
`f(x)=ab^x`

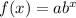
Where, a is the initial amount and b is the factor of rate.

If b>1, function has growth rate.

If b<1, function has decay rate.

We have given the function,
`N(t) = 300\cdot 2^{-(t)/(8)}`

Where, N represents the number of zombies and t is the number of years.

Applying properties of exponent,

`x^(-a)=(1)/(x^a)`

`N(t) = 300\cdot \frac{1}{2^{(t)/(8)}}`

`N(t) = 300\cdot ((1)/(2))^{(t)/(8)}`

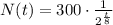
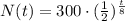
On comparing with general form of exponential function,

a=300 and
`b=(1)/(2)`

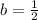
So,
`(1)/(2)<1\Rightarrow b<1`

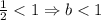
Which means the function is exponential decay.

Therefore, The given function is exponential decay.