Question

Which system of inequalities has a solution set that is a line?

Answer 1

The system of inequality that has a solution set that is a line is:

`x+y\geq 3\\\\x+y\leq 3`

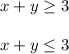
Explanation:

We know that if:

`a\leq b`

and

`a\geq b`

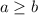
Then the resulting equation from both the inequalities is:

a=b

Hence, from the option (A) we have:

`x+y\geq 3--------(1)`

and
`x+y\leq 3-------------(2)`

Hence, the equation that is resulting from the above system of inequalities is:

`x+y=3`

( Since, the inequality (1) is a solid straight line passing through the point (0,3) and (3,0) and the shaded region is away from the origin, above the line.

and from inequality (2) we get a solid straight line passing through the point (0,3) and (3,0) and the shaded region is towards the origin, below the line )

Hence, the common region that satisfy from both the inequality is a line:

`x+y=3`

Answer 2

We're going to solve each of the systems to determine the solution.

System
`1`

`x+y \geq 3\\ x+y \leq 3`

using a graph tool

the solution is the line
`x+y=3`

see the attached figure N
`1`

System
`2`

`x+y \geq -3\\ x+y \leq 3`

using a graph tool

the solution is the shaded area

see the attached figure N
`2`

System
`3`

`x+y > 3\\ x+y < 3`

using a graph tool

The system has no solution

see the attached figure N
`3`

System
`4`

`x+y > -3\\ x+y < 3`

using a graph tool

the solution is the shaded area

see the attached figure N
`4`

therefore

the answer is

System
`1`

`x+y \geq 3\\ x+y \leq 3`