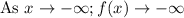Question

For the polynomial function ƒ(x) = −0.02x4 + .36x2 − 1.62, find all local and global extrema

Answer 1

dy/dx=-.08x^3+.72x

d2y/dx2=-.24x^2+.72

.08x(9-x^2) so we have extrema at x=-3,0,3

d2y/dx2 (-3)=-1.44, (0)=.72, (3)=-1.44

So you have two global maximums at (±3,0)

We have a local minimum at (0,-1.62)

There are no global minimums as the function decreases without bound as x approaches ±oo

Answer 2

Global maxima are (3, 0) and (-3, 0),

Local minima is (0, -1.62)

Explanation:

Here, the given function,

`f(x) = -0.02x^4+0.36x^2-1.62`

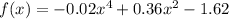
Differentiating with respect to x,

`f'(x) = -0.08x^3+0.72x`

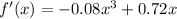
For maxima or minima,

`f'(x)=0`

`\implies-0.08x^3+0.72x=0`

`-0.08x(x^2-9)=0`

`\implies x=0\text{ or }x=\pm 3`

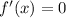
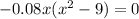
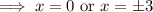
Thus, the critical points of the function f(x) are 0, -3 and 3,

Since, f'(x) > 0 on the left side of x = -3 and f'(x) < 0 on the right side of x = -3,

⇒ x = -3 is local maxima,

Also, f(-3) = 0,

⇒ f(x) has maxima at (-3, 0),

f'(x) < 0 on the left side of x = 0 and f'(x) > 0 on the right side of x = 0,

⇒ x = 0 is the local minima,

Also, f(0) = -1.62

⇒ function f(x) has minima at (0, -1.62),

Hence, the global maxima are (3, 0) and (-3, 0),

Local minima is (0, -1.62).

f'(x) > 0 on the left side of x = 3 and f'(x) < 0 on the right side of x = 3,

⇒ x = 3 is local maxima,

Also, f(3) = 0,

⇒ function f(x) has maxima at (3, 0).

Note : function f(x) has no global minima because its end behaviour is,

`\text{As }x\rightarrow \infty ; f(x)\rightarrow -\infty`

`\text{As }x\rightarrow -\infty ; f(x)\rightarrow -\infty`