Question

A missile is launched from the ground. Its height, h(x), can be represented by a quadratic function in terms of time, x, in seconds. After 1 second, the missile is 130 feet in the air; after 2 seconds, it is 240 feet in the air. Find the height, in feet, of the missile after 11 seconds in the air.

Answer 1

h(11) = 330 ft

Explanation:

We have 2 points with which to find the equation of the projectile. The standard form for the quadratic, which is the function that models parabolic motion, is

`h(x)=ax^2+bx+c`

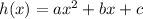
The problem tells us that the missile was launched from the ground, so c (the initial height of the missile) is 0, so we can literally disregard the c in the standard form and use the 2 points to solve for a and b:

At the point (1, 130) we fill in the standard form to get:

`130=a(1)^2+b(1)`

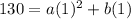
which gives us **130 = a + b**. Now on to the second point, (2, 240):

`240=a(2)^2+b(2)`

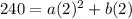
which gives us **240 = 4a + 2b**

Solve the first **equation for a:

a = 130 - b

and sub that into the second **equation:

240 = 4(130 - b) + 2b and simplify to

140 = b

Now that we know b, we can sub it in to solve for a:

a = 130 - b so a = 130 - 140 so a = -10. Therefore, the equation of the projectile's motion is

`h(x)=-10x^2+140x`

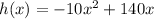
(If you knew your Physics, you'd know that -10x^2 is replacing the pull of gravity in the metric system which is -9.8x^2; that's how we know that this is the correct equation.)

Subbing in 11 for x:

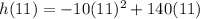`h(11)=-10(11)^2+140(11)` gives us that h(11) = 330 feet