Answer:
Hence, x=2 is a true solution and not a extraneous solution.
Explanation:
We know that:
Extraneous solution is a solution which is obtained by solving the equation but does not hold true in the original equation.
We have to find the solution of the algebraic equation which is given as:
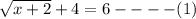
Now we will keep the constant term, on one side of the equation to obtain:
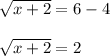
Now on squaring both side of the equation we get:
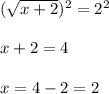
Hence, we get a solution as x=2.
Hence, on putting x=2 in equation (1) we obtain:
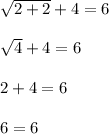
Hence, x=2 is a true solution.